Geometrinin en temel konuları içerisinde özel üçgenler gelir. Belli ve standart formülü üzerinden ele alınan özel üçgenler, birçok farklı kenar ve açının bulunmasında önemli bir kolaylık sağlamaktadır. Özel üçgenler genelde açı ve kenarlarının sabit rakamları üzerinden ele alınmak suretiyle ifade edilir. Bu sayede çok daha kolay bir şekilde işlem yapılabilmekte ve sonuç ortaya çıkarabilmektedir. Tabii geometride yer alan tüm özel üçgenlerin kendi açıdan farklı özellikleri bulunur.

Haberin Devamı

Haberin Devamı

Haberin Devamı

Haberin Devamı

Özel Üçgenler Nelerdir?

Kendi özellikleri ve yapılarına sahip olan özel üçgenler genel anlamda 3 farklı şekilde ele alınmalıdır.

- Dik üçgenler
- İkizkenar üçgenler
- Eşkenar üçgenler

Yukarıdaki gibi üç gruba ayrılan özel üçgenler kenarları ile beraber açıları noktasında kendine has özellikler ortaya çıkarmaktadır. Böylece sabit ve standart bir yapı altında ele alınan özel üçgenler, geometri üzerinden birçok farklı işlemi kolayca gerçekleştirme imkanı tanımaktadır.

Özel Üçgen Örnekleri ve Özellikleri…

Üç grup eşliğinde öne çıkan özel üçgenler birçok farklı özelliği ile beraber ayrılmaktadır.

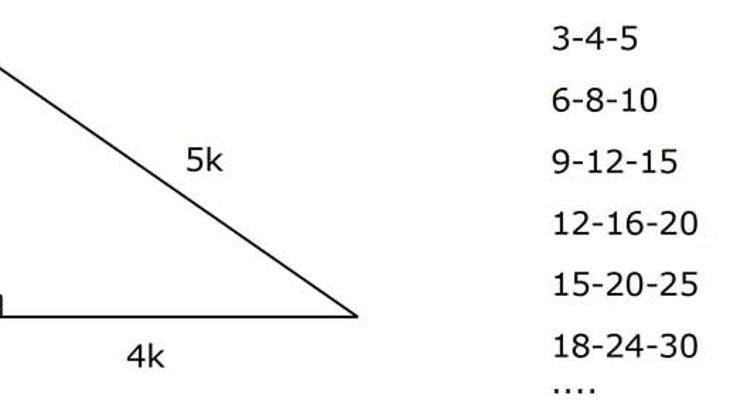
Dik üçgenler: İç açılarından biri 90 derece olan üçgene dik üçgen denmektedir. İç açıları 180 derecedir ve dış açıları ise 360 derecedir. Aynı zamanda 90 derecenin karşısındaki kenara ise hipotenüs olarak ifade edilmektedir. Bu konudaki hipotenüs üçgenin her zaman en büyük kenarı olarak bilinir.

İkizkenar üçgenler: Adından da anlaşılacağı üzere iki kenarı aynı olan üçgenler ikizkenar üçgen olarak ifade edilmektedir. Aynı uzunluğa sahip iki kenarın kesiştiği açı farklı derecede üzerinden ele alınabilmektedir. Köşegeninden bir dikme inildiği vakit, karşı kenarı ikiye böler.

Eşkenar üçgenler: Eşkenar üçgenler ise bütün kenarlarının aynı uzunluğa sahip olduğu üçgenlerdir. Bütün iç açıları birbirine eşittir ve her biri 60 derecedir. Bu şekilde iç açıları toplamda 180 derece olur.

Özel Üçgenlerin Kullanımı

Özel üçgenler hem kilometre içerisinde hem de birçok farklı matematik formülü ile beraber analitikte kullanılmaktadır. Aynı zamanda çember açısından yapılacak çizim ile beraber işlem yapma imkanı sağlar. Sabit kenarları ve açıları olduğundan dolayı, bazı kenar ve açılar bilindiği vakit kolayca işlem yapma imkanı sağlar.